Circle Rasterization

Investigation on fast grid-aligned circle rasterization.

– Created: January 24, 2025 UTC

– Tags: Programming, Optimization, C

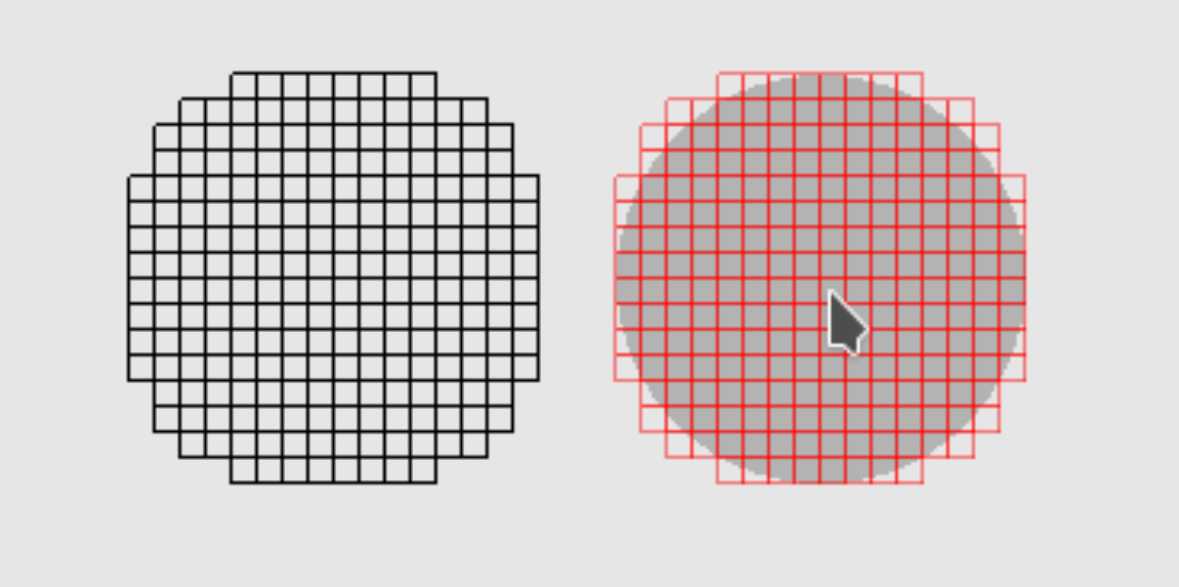
Currently drastically overthinking anything related to dream Minecraft-like game of mine, and today it was all about chunk loading. Particularly, ideal way to infer which chunks should be loaded based on distance to the viewer, instead of typical direct grid.

For that circle rasterization is needed. I came up with following pieces of code, one reusable macro, and others are meant to be directly copy pasted where needed:

Macro:

/* Emits `x` and `y` for every intersecting cell */
/* We snap position to the nearest corner, which means there's no aliasing */
/* It works great for integer radii */
#define m_iter_circle_pixels(p_center_x, p_center_y, p_radius) \
    for (float y = (p_center_y + ceilf(p_radius)) - 1; y > (p_center_y - ceilf(p_radius)) - 1; --y) \
        for (float x = p_center_x - ceilf(sqrtf(p_radius * p_radius - (y - p_center_y + (y <= p_center_y)) * (y - p_center_y + (y <= p_center_y)))); \
                   x < p_center_x + ceilf(sqrtf(p_radius * p_radius - (y - p_center_y + (y <= p_center_y)) * (y - p_center_y + (y <= p_center_y)))); ++x)

Floating point based one:

float const rs = state->r * state->r;
float const cr = ceilf(state->r);
for (float iy = -cr; iy <= cr - 1; ++iy) {
    float const dx = ceilf(sqrtf(rs - (iy + (iy <= 0)) * (iy + (iy <= 0))));
    for (float ix = -dx; ix < dx; ++ix) {
        /* iy and ix are floating point offsets from (0, 0) */
    }
}

Integer math based one:

/* Neat shorthand making integer based loops drastically faster */
static int32_t ceil_sqrt(int32_t const n) {
    int32_t res = 1;
    #pragma clang loop unroll_count(8)
    while(res * res < n)
        res++;
    return res;
}

/* This one beats the float in raw performance, but might scale worse at increasing radii, assuming sqrt is a hardware intrinsic with known worst time */
int32_t const rsi = (int32_t)state->r * (int32_t)state->r;
for (int32_t iy = -(int32_t)state->r; iy <= (int32_t)state->r - 1; ++iy) {
    int32_t const dx = ceil_sqrt(rsi - (iy + (iy <= 0)) * (iy + (iy <= 0)));
    for (int32_t ix = -dx; ix < dx; ++ix) {
        /* iy and ix are integer offsets from (0, 0) */
    }
}

Integer math based with accumulated ceil(sqrt()), the fastest I could come up with:

int32_t const rsi = (int32_t)state->r * (int32_t)state->r;
int32_t acc = 1;
for (int32_t iy = (int32_t)state->r - 1; iy >= 0; --iy) {
    while (acc * acc < rsi - iy * iy) acc++;
    for (int32_t ix = -acc; ix < acc; ++ix) {
        /* lower portion */
        x = (float)ix;
        y = (float)iy;
        /* upper portion */
        x = (float)ix;
        y = (float)-iy - 1;
    }
}

Note that they assume center point at coordinate origin, quadrant symmetry and whole number radii.

Benchmarks:

Profile 'float'         on average took: 0.001537s, worst case: 0.003272s, sample count: 277
Profile 'int32_t'       on average took: 0.000726s, worst case: 0.002293s, sample count: 277
Profile 'int32_t acc'   on average took: 0.000650s, worst case: 0.001732s, sample count: 277